Machine Learning Algorithms (A quick revision)

there is only 4 algorithms :
Linear Regression
Logistic Regression
Decision Tree
Random Forest

Steps for Machine Learning Algorithms

1. Define the Problem: Identify the task and the kind of data needed to address it (e.g., classification, regression).

2. Collect Data: Gather relevant data for your algorithm to learn from.

3. Preprocess Data: Clean, normalize, or encode data to prepare it for analysis.

4. Split the Data: Divide data into training, validation, and testing datasets.

5. Select an Algorithm: Choose an appropriate model (e.g., decision trees, neural networks).

6. Train the Model: Use training data to let the algorithm learn patterns.

7. Validate the Model: Use the validation set to fine-tune and improve performance.
   Prediction and Evaluation steps is necessary model accuracy.

8. Test the Model: Evaluate how well the algorithm performs on new, unseen data.

9. Deploy the Model: Implement it in a real-world environment if it meets accuracy criteria.

10. Monitor & Update: Regularly monitor performance and update the model if needed.

Now we are talking about the algorithms in machine learning.

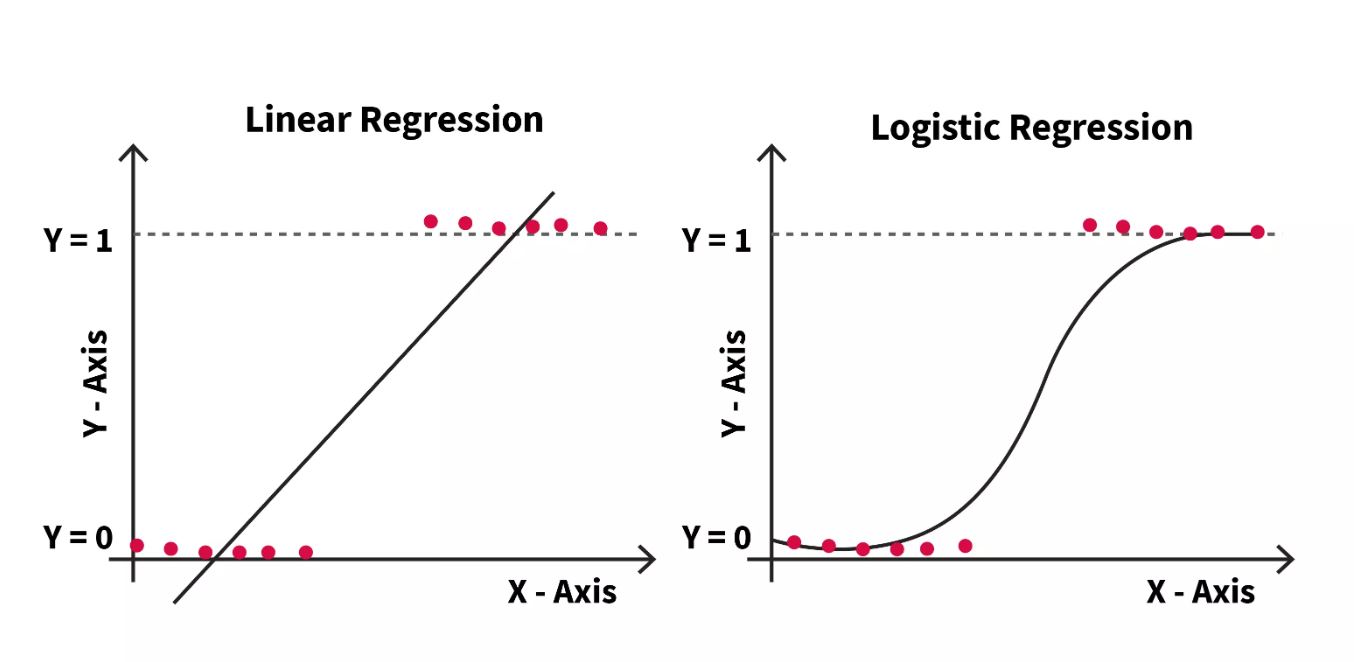
Linear Regression

• It predicts real values (or) Predicting output variable is "continuous data".
• A relationship is established between the independent variable and the dependent variable by fitting a best fit line.
• Assuming the relation between x & y is "linear" (or) The best fit line is known as the "regression line".

Representation:

y = mx + c

Where:

• y = dependent variable
• m = slope
• x = independent variable
• c = intercept

Y = β0 + β1X1 + β2X2 + ... + βpXp

Where:

• Y: The response variable.
• Xj: The jth predictor variable.
• βj: The average effect on Y of a one-unit increase in Xj, holding all other predictors fixed.

Logistic Regression

• It is a classification algorithm used to estimate "Discrete Data values" based on a given set of independent variables.
• Its output value lies between [0 and 1] or [yes/no].
• Uses the Sigmoid function probability:
• Whereas logistic regression is used to calculate the probability of an event. For example, classify if tissue is benign or malignant.
• Logistic regression assumes the binomial distribution of the dependent variable.

e^y/(1+e^y) 


p(X) = e^(β0 + β1X1 + β2X2 + ... + βpXp) / (1 + e^(β0 + β1X1 + β2X2 + ... + βpXp))

Decision Tree

• It is a Supervised learning algorithm used for classification problems.
• Works with both categorical and continuous dependent variables.
• In this algorithm, the "population is split" into two (or) more homogeneous sets based on conditions.

Different Techniques:

• Gini impurity
• Information Gain
• Chi-square
  Code (if need)

from sklearn.tree import DecisionTreeClassifier

# Create a decision tree classifier
dt = DecisionTreeClassifier(criterion='entropy', random_state=42)

# Fit the model
dt.fit(X_train, Y_train)

# Predict on the test set
dt_pred = dt.predict(X_test)

Pros:

• Interpretability: Easy to visualize and understand.
• Speed: Quick to train and make predictions.

Cons:

• Overfitting: Prone to overfitting, especially with deep trees.
• Sensitivity to Outliers: Can be heavily influenced by outliers.

Random Forest

• A collection of Decision Trees is called a "Random Forest".
• To classify a new object based on its attributes:
  • Each tree in the forest provides a classification.
  • The majority of votes determines the final class (this is known as the Bagging Technique).
• Applicable for both Classification and Regression tasks.

Code (if need)

from sklearn.ensemble import RandomForestClassifier

# Create a random forest classifier
rf = RandomForestClassifier(n_estimators=100, random_state=42)

# Fit the model
rf.fit(X_train, Y_train)

# Predict on the test set
rf_pred = rf.predict(X_test)

Pros:

• Accuracy: Generally more accurate than a single decision tree.
• Robustness: Less sensitive to outliers and noise.
• Overfitting: Less prone to overfitting due to ensemble averaging.

Cons:

• Interpretability: Difficult to interpret and visualize.
• Computation: Requires more computational resources and time to train.

Thanks for Reading ~ Jai hanuman