Loss in Regression
On this page
Loss
Distance of loss
Types of Loss
Functional Difference Between L1 Loss and L2 Loss (MAE and MSE)
Relationship Between the Model and the Data
question
Loss in Equations
Loss is a numeric metric that describes how wrong a model's predictions are. Loss measures the distance between the model's predictions and the actual labels. The goal of training a model is to minimize the loss, reducing it to its lowest possible value.
Distance of Loss
In statistics and machine learning, loss measures the difference between the predicted and actual values. Loss focuses on the distance between the values, not the direction.
Example
If a model predicts 2, but the actual value is 5, we don't see that the loss is negative -3 (2-5=-3). Instead, we care that the distance between the values is 3. Thus, all methods for calculating loss remove the sign.
The two most common methods to remove the sign are the following:
- Take the absolute value of the difference between the actual value and the prediction.
- Square the difference between the actual value and the prediction.
Types of Loss
In linear regression, there are four main types of loss, which are outlined in the following table:
| Loss Type | Definition | Equation |
|---|---|---|
| L1 Loss | The sum of the absolute values of the difference between the predicted values and the actual values. | Sigma(actual value - predicted value) |
| Mean Absolute Error (MAE) | The average of L1 losses across a set of examples. | 1/N(Sigma(actual value - predicted value) ) |
| L2 Loss | The sum of the squared difference between the predicted values and the actual values. | (Sigma(actual value - predicted value)^2 ) |
| Mean Squared Error (MSE) | The average of L2 losses across a set of examples. | 1/2Sigma(actual value - predicted value)^2 ) |
Functional Difference Between L1 Loss and L2 Loss (MAE and MSE)
The functional difference between L1 loss and L2 loss (or between MAE and MSE) is squaring. When the difference between the prediction and label is large, squaring makes the loss even larger. When the difference is small (less than 1), squaring makes the loss even smaller.
When processing multiple examples at once, we recommend averaging the losses across all the examples, whether using MAE or MSE.
Best of MSE and MAE
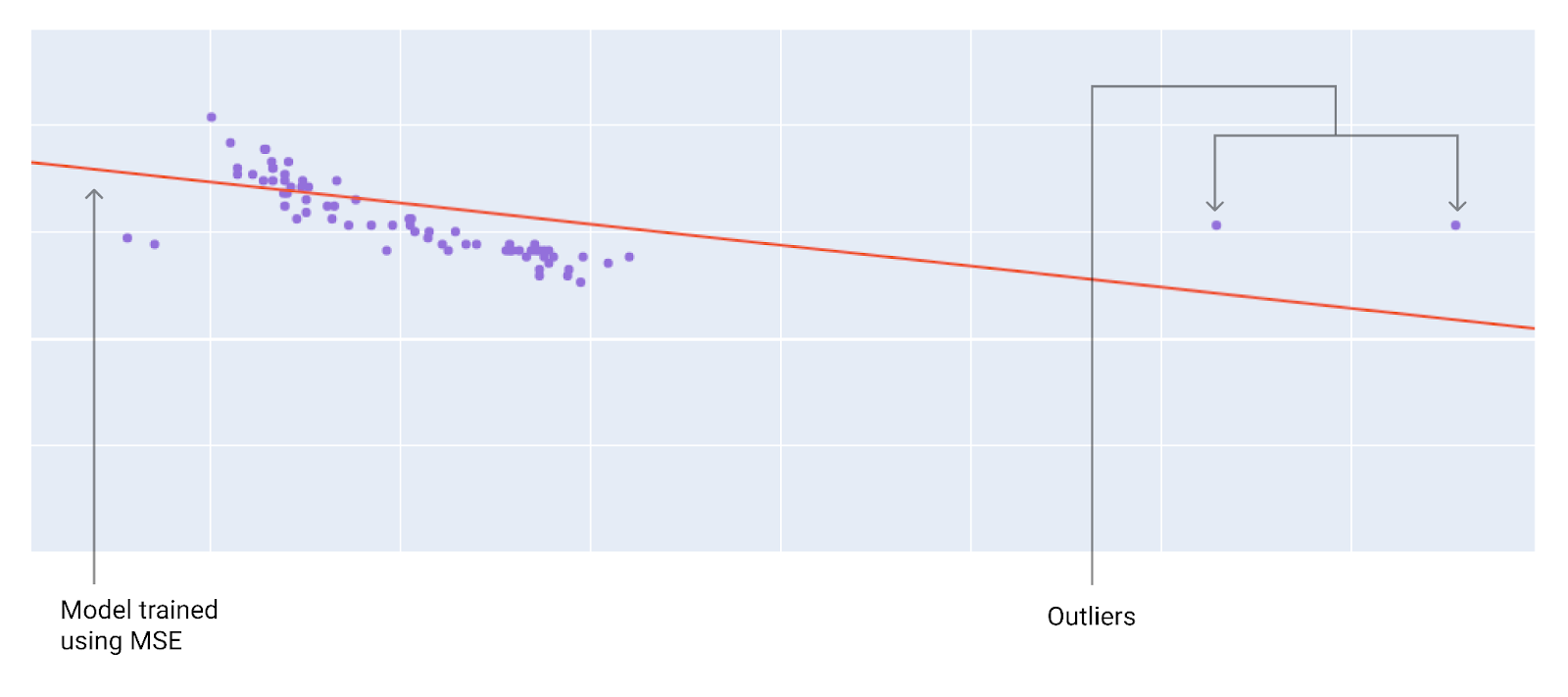
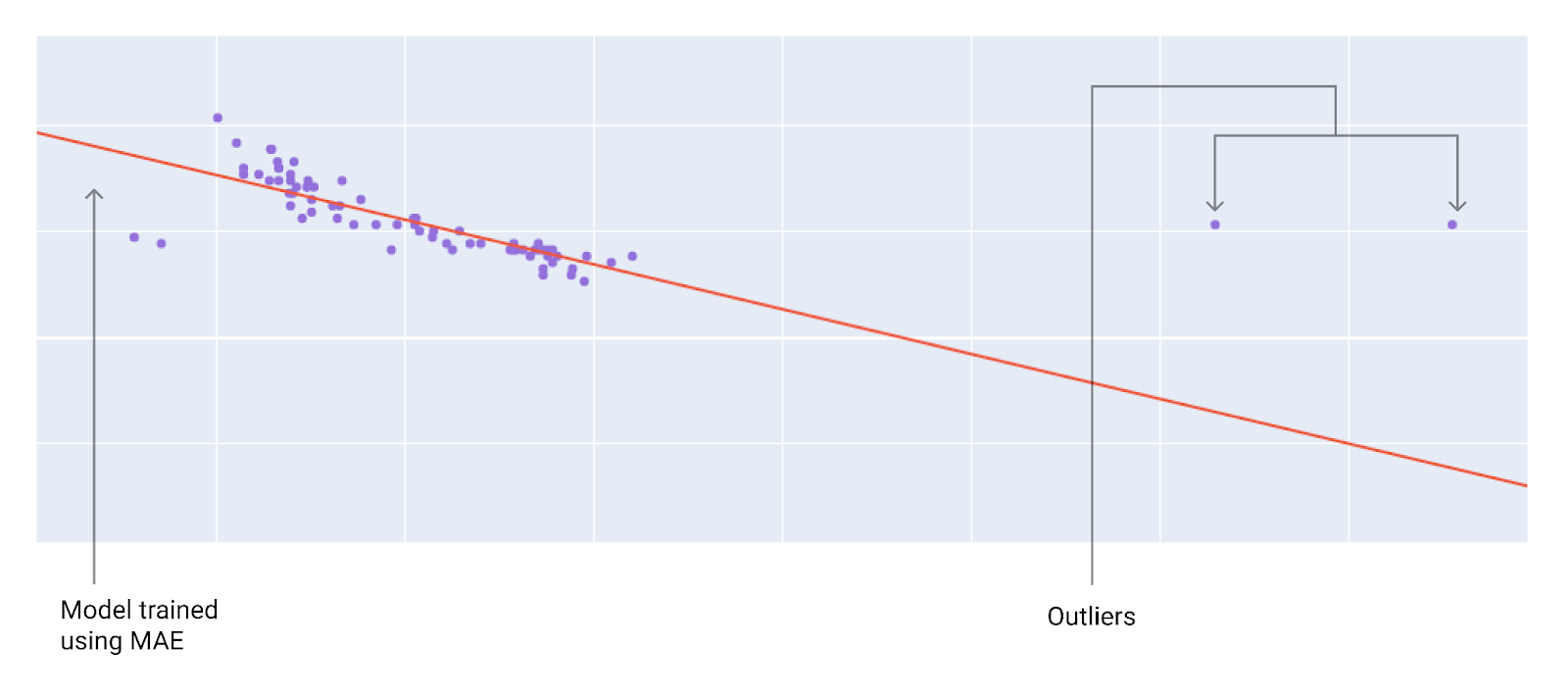
When choosing the best loss function, consider how you want the model to treat outliers. For instance, MSE moves the model more toward the outliers, while MAE doesn't. L2 loss incurs a much higher penalty for an outlier than L1 loss. For example, the following images show a model trained using MAE and a model trained using MSE. The red line represents a fully trained model that will be used to make predictions. The outliers are closer to the model trained with MSE than to the model trained with MAE.
Diagram : A model trained with MSE moves the model closer to the outliers.
and Diagram : A model trained with MAE is farther from the outliers
Relationship Between the Model and the Data
-
Mean Squared Error (MSE): The model's predictions align more closely with the outliers in the dataset, but this comes at the cost of being further away from the majority of other data points. This is due to the squaring operation in the loss calculation, which amplifies the effect of larger errors (outliers).
-
Mean Absolute Error (MAE): The model's predictions are less influenced by outliers, resulting in a better fit to most of the data points. This is because MAE uses absolute values, treating all deviations equally regardless of their magnitude.
Question Session
What is SSE?
SSE = Sum of Squares of Error
Denoted by:
*Σ[(Y - Y)^2] = SSEmin
Where:
- Y : Actual value
- ** Y* : Predicted value
This value should be minimum
Problem with Mean Square Error (MSE)
Problem:
problem with MSE is with calculating of d/dx of x^2 we will get some value of error . Units are also squaring up it gives wrong prediction. Therefore, we often avoid using MSE.
Solution:
The solution to this problem is:
*RMSE = sqrt((sigma(Y-Y)^2)/N)
2 Reactions
0 Bookmarks